בפוסט הקודם הצגנו את מודל בלאק ושולס וראינו שהמודל מורכב מ 5 פרמטרים: נכס הבסיס, מחיר מימוש האופציה, הזמן עד הפקיעה, שער הריבית חסרת הסיכון במשק וסטיית התקן הגלומה. ראינו גם שלכל פרמטר יש את היווניות הבוחנות את ההשפעה על מחיר האופציה בהינתן שינוי של פרמטר ספציפי כאשר כל שאר הפרמטרים נותרים זהים. הפעם אני רוצה להרחיב על פרמטר מימד הזמן, היוונית תטא, פרמטר שער הריבית חסרת הסיכון והיוונית רו.
על מנת להמחיש את התנהגות היווניות שנדבר עליהן הפעם, אני מצרף את התמונה מהפוסט הקודם. ממליץ לפתוח אותה בטאב חדש בכדי לראות בבירור.
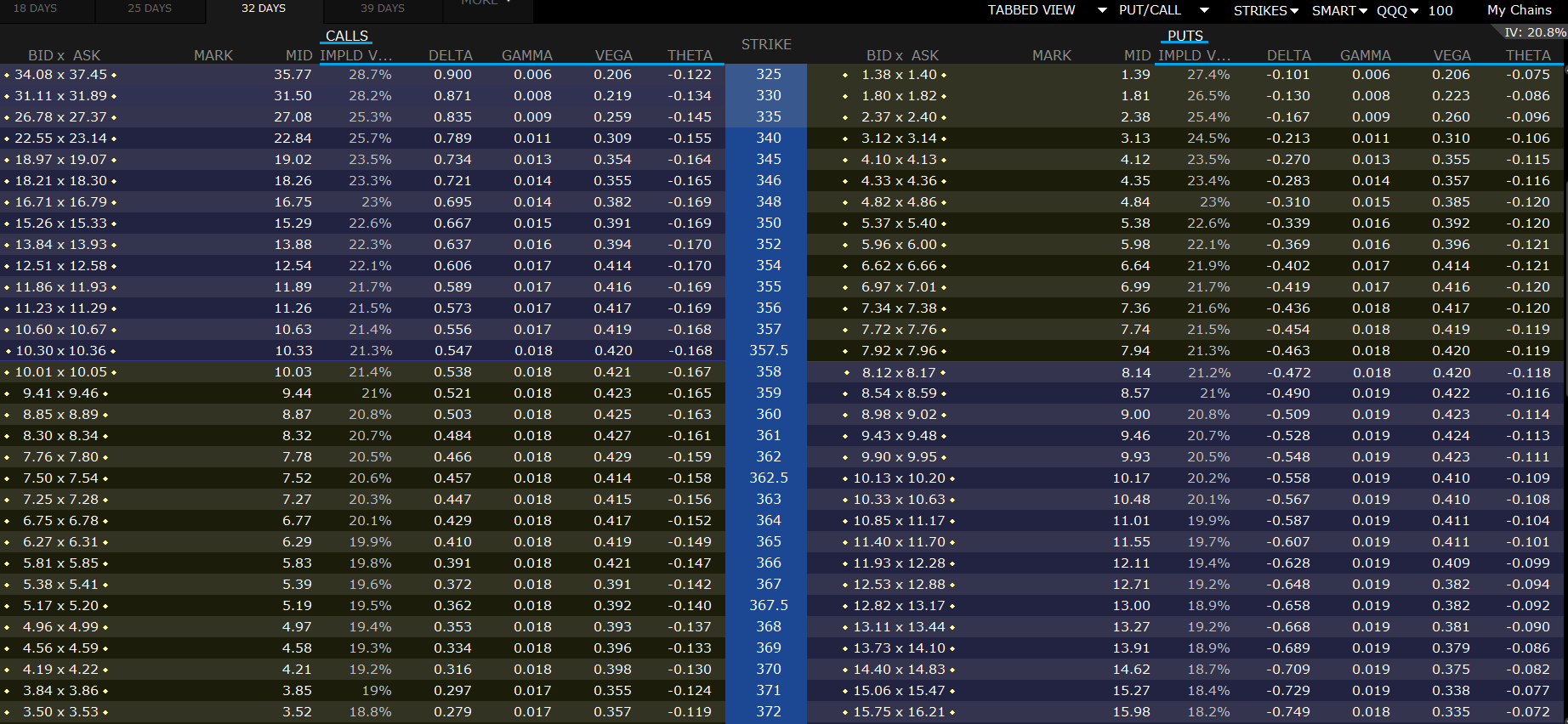
הזמן עד הפקיעה
לאופציה יש זמן חיים מוגבל שהוא עד תאריך הפקיעה, אופציה לא נשארת איתנו “לנצח” כמו נכס בסיס. בפקיעה האופציה יכולה להפוך לנכס בסיס או להעלם. הזמן הוא מרכיב מאוד משמעותי בתמחור מחיר האופציה שכן הוא אומר לנו בכמה נשחקת האופציה בכל יום שעובר. ניקח לדוגמה את מניית AMZN שנסחרת כרגע ב 130$, נרכוש 2 אופציות CALL לאותו סטרייק של 150$ אבל עם תאריך פקיעה שונה, אופציה אחת תפקע עוד יומיים והאופציה השניה תפקע עוד חודשיים. האופציה של עוד יומיים תהיה זולה משמעותית מהאופציה של עוד חודשיים כיוון שהסיכוי שהמניה תעלה 20$ ביומיים מאוד נמוך מהסיכוי שהמניה תעלה 20$ בחודשיים. ככל שהזמן לפקיעה ארוך יותר כך קיימת האפשרות לתנודות גדולות יותר במחיר נכס הבסיס ולכן מחירי האופציות עולים, כי ההסתברות לפקיעה בתוך הכסף עולה. גם כאן, את הזמן לפקיעה אנחנו קובעים ויודעים מראש, יש לנו וודאות לגבי כמה זמן נשאר לאופציה לחיות.
היוונית תטא
התטא היא האות היוונית שמייצגת לנו את השחיקה הצפויה בערך האופציה עקב התקצרות של יום בזמן הפקיעה. היא אומדן לירידה בערך האופציה כפונקציה של שינוי בערך הזמן, כל האופציות מאבדות מערכן ככל שזמן המימוש קרב (כי נשאר פחות זמן לסיכוי של התנועה שתכניס את האופציה לכסף). לדוגמה, נסתכל על CALL 371$ בתמונה שנסחר כרגע באזור 385$, התטא שלו היא מינוס 0.124. בהנחה ושום פרמטר אחר לא השתנה ועבר רק יום אחד, מחיר האופציה אמור לרדת ב 12.4$ ל 372.6$. התטא שלילית כאשר אנחנו בפוזיציית LONG וחיובית כאשר אנחנו בפוזיציית SHORT. התטא הולכת וגדלה ככל שהזמן לפקיעה קטן וקטנה ככל שהזמן לפקיעה גדל.
שער הריבית חסרת הסיכון
במודל הנאיבי לתמחור אופציות ראינו ששער הריבית חסרת הסיכון מהווה חלק אינטגרלי ממודל ה PCP, גם כאן יש לשער הריבית השפעה על התמחור. ככל ששער הריבית במשק גבוה יותר כך מחירי האופציות עולים. ממשבר הסאב-פריים ועד לתקופת הקורונה חווינו ריבית אפסית במשק מה שהוביל לכך שמחירי האופציות כמעט ולא תמחרו את הריבית. גם כאן, שער הריבית החסרת סיכון (ריבית הפד/בנק ישראל) ידועה מראש.
היוונית רו
הריבית חסרת הסיכון במשק היא חלק בלתי נפרד גם ממודל בלאק ושולס ויש לה אפילו אות יוונית משל עצמה. היוונית רו (Rho) מייצגת את השינוי במחיר האופציה כאשר הריבית חסרת סיכון במשק תשתנה ב 1%. באופציית CALL, ככל ששער הריבית עולה כך ערך אופציית ה CALL עולה ובאופציית PUT ככל ששער הריבית עולה ערך אופציית ה PUT יורד. כסוחרים, הרו פחות רלוונטית עבורנו אלא אם אנחנו רוכשים אופציות שנים קדימה. בתמונה אין עמודה ליוונית רו.
לסיכום, הפעם הרחבנו על הפרמטרים הנוספים שמודל בלאק ושולס מקבל. ראינו כיצד מימד הזמן שוחק לנו את האופציה ואיך שער הריבית חסרת הסיכון במשק יכולה לשפיע על תמחורי האופציות. בפרק הבא נדבר על סטיות התקן והתנודתיות – החלק הכי מעניין.
בלוג זה נוצר בכדי ללמד, להעשיר ולחלוק את רעיונותיי ואת דעותיי האישיות בלבד. אין בנכתב המלצה לפעולה והמידע הינו אינפורמטיבי ולימודי בלבד – כל העושה שימוש בתכנים / רעיונות המועלים בפוסט זה עושה זאת על דעת עצמו ואחריותו הבלעדית. שימוש באופציות ללא ידע וניסיון מקדים עלול להוביל למחיקת התיק ולהגדלת חשיפת הסיכון.
